If you are familiar with machine learning, you might have heard the term hypothesis. Have you wondered what that means? A hypothesis can be described as the assumptions that map the input to the output. The terms “hypothesis” and “model” are sometimes used interchangeably. However, a hypothesis represents an assumption, while a model is a mathematical representation employed to test that hypothesis.
Hypothesis in machine learning
A hypothesis in machine learning is an educated guess or assumption about how the input features (data) are connected to the results (outputs or predictions). It represents the model’s idea of the mapping function that links inputs to outputs, which the algorithm is trying to learn from the training data.
How It Works
- Initial Guess: We start with an initial guess or model that we think might explain the relationship between the input features and the outputs.
- Training: Using the training data, we test this guess. The algorithm adjusts the parameters (like weights in a neural network) to reduce the difference between the predicted outputs and the actual outputs.
- Optimization: The goal is to find the best parameters that make the model’s predictions as accurate as possible on new, unseen data.
- Evaluation: A cost function (or loss function) is used to measure how well the hypothesis (model) is performing. The lower the cost, the better the hypothesis.
Hypothesis Space in Machine Learning
The hypothesis space is the set of all possible hypotheses (models) that can be used to make predictions based on the input data. In other words, it includes all the possible ways we can guess the relationship between the features and the target variable.
To better understand the Hypothesis Space and Hypotheses, consider the following scenario:
Imagine we have some data points distributed across a coordinate plane. We want to determine the output or category for each point based on its position in the plane. There could be multiple hypotheses that fit the data. Here are a few examples:
1. Initial Hypothesis(Hypothesis 1)
We might decide to divide the coordinate plane with a vertical line. Points to the left of the line belong to one category, while points to the right belong to another category.
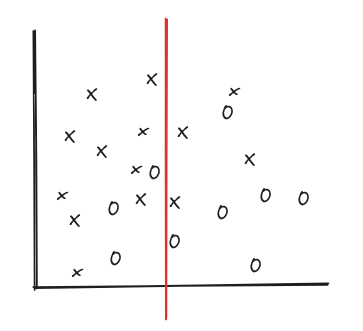
2. Another Hypothesis(Hypothesis 2)
Alternatively, we could divide the plane using a horizontal line. Points above the line belong to one category, and points below belong to another category.
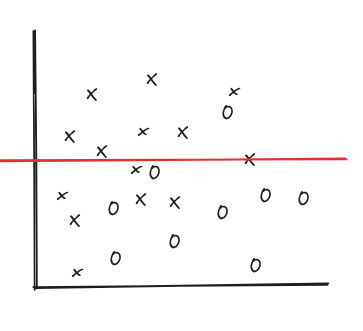
We might choose to use a diagonal line to divide the plane. Points on one side of the diagonal belong to one category, while points on the other side belong to another category.
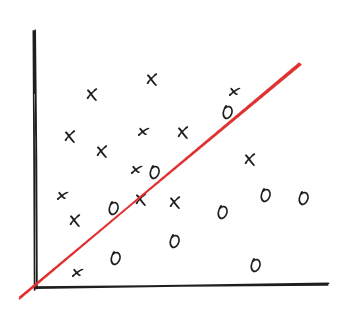
The set of all these possible hypotheses forms the Hypothesis Space. Each individual possible way to divide the coordinate plane and categorize the points is known as a hypothesis.
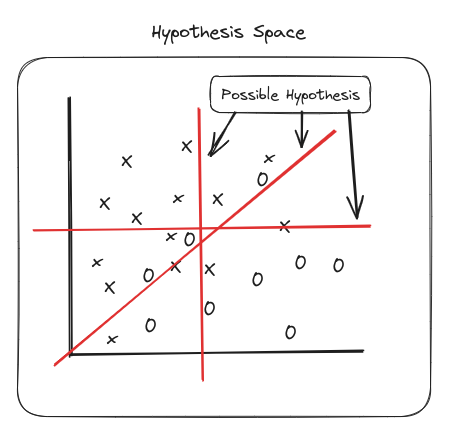
Hypothesis Evaluation
Evaluation is a crucial step in understanding how well a hypothesis (or model) performs. It involves measuring the accuracy of the predictions made by the model using specific metrics. For regression problems, common evaluation metrics include:
- Mean Squared Error (MSE): Measures the average squared difference between predicted and actual values.
- Root Mean Squared Error (RMSE): The square root of MSE, providing an error metric in the same units as the target variable.
- Mean Absolute Error (MAE): The average of absolute differences between predicted and actual values.
- R-squared ($R^2$): Represents the proportion of variance in the dependent variable that is predictable from the independent variable(s).
For classification problems, common evaluation metrics include:
- Accuracy: The ratio of correctly predicted instances to the total instances.
- Precision: The ratio of correctly predicted positive observations to the total predicted positives.
- Recall (Sensitivity): The ratio of correctly predicted positive observations to all observations in the actual class.
- F1 Score: The harmonic mean of precision and recall, providing a single metric that balances both.
Hypothesis Testing
Testing a hypothesis involves using a separate set of data, known as the test set, which was not used during the training phase. This step is essential to ensure that the model generalizes well to new, unseen data. The process typically includes:
- Splitting the Data: The data is split into training and testing sets, often with a ratio of 70/30 or 80/20.
- Training the Model: The model is trained using the training set.
- Making Predictions: The trained model makes predictions on the test set.
- Evaluating Performance: The predictions on the test set are compared to the actual outcomes to evaluate the model’s performance using the metrics discussed earlier.
Generalization
Generalization refers to the model’s ability to perform well on new, unseen data. A model that generalizes well captures the underlying patterns in the data without overfitting to the noise in the training set. Generalization is crucial for ensuring that the model remains useful beyond the specific dataset it was trained on. Key concepts related to generalization include:
- Overfitting: When a model learns the training data too well, capturing noise and specific patterns that do not generalize to new data. Overfitting leads to high accuracy on the training set but poor performance on the test set.
- Underfitting: When a model is too simple to capture the underlying patterns in the data, resulting in poor performance on both the training and test sets.
- Bias-Variance Tradeoff: This tradeoff helps in balancing underfitting and overfitting. High bias (underfitting) and high variance (overfitting) need to be balanced to achieve optimal generalization.
Techniques to Improve Generalization
- Cross-Validation: A technique where the data is divided into multiple folds, and the model is trained and validated on different folds iteratively. This helps in ensuring the model’s performance is consistent across different subsets of the data.
- Regularization: Adding a penalty to the cost function to discourage overly complex models. Common regularization techniques include L1 (Lasso) and L2 (Ridge) regularization.
- Hyperparameter Tuning: Carefully selecting and optimizing hyperparameters (such as learning rate, depth of a decision tree, etc.) to improve model performance and generalization.
- Early Stopping: In iterative training processes like neural networks, stopping the training process when the performance on the validation set starts to degrade helps prevent overfitting
Thanks for reading
Thank you for taking the time to read this blog post. I hope you found the information valuable and insightful. Your support means a lot, and I appreciate your interest. – Rocktim Sharma
